Numbers are commutative, since xy = y x and x y = y x for all real numbers x and y However the operation of subtraction is not commutative, since x y 6=y x in general (Indeed the identity x y = y x holds only when x = y) 33 Associative Binary Operations Let be a binary operation on a set A Given any three elements x, y andFor example, the polynomial identity (x 2 y 2) 2 = (x 2 – y 2) 2 (2xy) 2 can be used to generate Pythagorean triples Suggested Learning Targets Understand that polynomial identities include but are not limited to the product of the sum and difference of two terms, the difference of two squares, the sum and difference of two cubes, theExample 3 Identity Property 6 0 = 6 x 0 = x (a b) 0 = a b Example 4 Additive Inverse Property 3 (3) = 0 x (x) = 0 If x = y, then y = x 3 If x = y and y = 7, then x = 7 4 6 2 = 2 6 5 5 ∙ 2 = 2 ∙ 5 6 10 (3 2) = (10 3) 2 7 6(3 ∙ 5) = (6 ∙ 3)5

Using Identity Viii X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Solve The Following Question 8x3 Y3 27z3 18xyz Maths Polynomials Meritnation Com
(x+y)^3 identity class 9
(x+y)^3 identity class 9-5 Theorem38 Let R be a ring with identityand a;b 2 RIfais a unit, then the equations ax = b and ya=b have unique solutions in R Proof x = a−1b and y = ba−1 are solutions check!Trigonometric Identities Solver \square!




Solved Questions 1 Demonstrate By Means Of Truth Tables Chegg Com
Factor x^3y^3 x3 − y3 x 3 y 3 Since both terms are perfect cubes, factor using the difference of cubes formula, a3 −b3 = (a−b)(a2 abb2) a 3 b 3 = ( a b) ( a 2 a b b 2) where a = x a = x and b = y b = y (x−y)(x2 xyy2) ( x y) ( x 2 x y y 2)Therefore, x = 40 and y = 2 deishlies12 deishlies12 Mathematics High School answered Find the value of 423 using the identity (x y)3 = x3 3x2y 3xy2 y3 1 See answer AdvertisementIt is read as $x$ plus $y$ whole cube It is mainly used in mathematics as a formula for expanding cube of sum of any two terms in their terms ${(xy)}^3$ $\,=\,$ $x^3y^33x^2y3xy^2$ Proofs The cube of $x$ plus $y$ identity can be proved in two different mathematical approaches Algebraic method Learn how to derive the expansion of cube of $x$ plus $y$ identity by the
These identities are useful whenever expressions involving trigonometric functions need to be simplified An important application is the integration of nontrigonometric functions a common technique involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identityTherefore, x = 50 and y = 3 I dont get this at all?In the system of mathematics, the identity is always an equation which is an equilibrium relation X= Y and Y = X, X and Y are the variables and X and Y provides the similar value as each other despite whatever values they are (most probable numbers) are replaced for the variables Read about the types of Additive and Multiplicative Identity at Vedantucom
411 Hyperbolic Functions The hyperbolic functions appear with some frequency in applications, and are quite similar in many respects to the trigonometric functions This is a bit surprising given our initial definitions Definition 4111 The hyperbolic cosine is the function cosh x = e x e − x 2, and the hyperbolic sine is theIn the LHS of the identity,we put x=2&y=3 Similarly in the RHS of the identity,we put x=2&y=3 Thus, the identity is verified Now, let's expand the second Identity If we replace ywith (−y)the expression changes to (x−y)3 So to find the expansion of (x−y)3, we can replace ywith (−y)in (xy)3=x23x2y3xy2y3Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Learn Algebraic Identities Of X Y And X Y In 3 Minutes
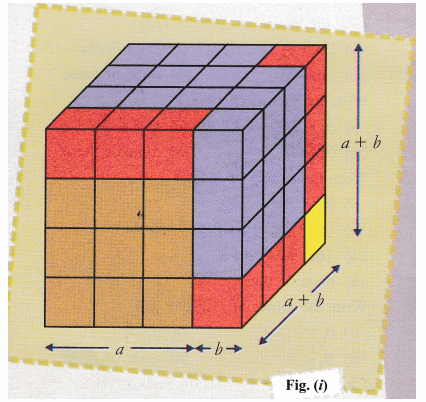
View 305 Algebra 2pdf from ALGEBRA 10 at Florida Virtual School 305 Polynomial identity's and properties By Ben Floyd Identity's chosen • column A (X y ) • column B (X ^2 2XY y ^2These go along with the Algebraic Proofs!! (9) Verify (i) x 3 y 3 = (x y) (x 2 − xy y 2) (ii) x 3 – y 3 = (x − y) (x 2 xy y 2) using some nonzero positive integers and check by actual multiplicationCan you call these as identites ?




Ex 9 4 3 Vi Simplify X Y X 2 Xy Y 2 Chapter 9 Class 8




Entering Identities And The Problem Type Download Scientific Diagram
Xy 2 cos x y 2 sinx siny= 2sin x y 2 cos xy 2 cosx cosy= 2cos xy 2 cos x y 2 cosx cosy= 2sin xy 2 sin x y 2 The Law of Sines sinA a = sinB b = sinC c Suppose you are given two sides, a;band the angle Aopposite the side A The height of the triangle is h= bsinA Then 1If a This video shows how to evaluate using the identity '(xy)3=x3y33x2y3xy2'To view more Educational content, please visit https//wwwyoutubecom/appuserie(i) To prove x 3 y 3 = (x y) (x 2 – xy y 2) Now, using identity VI we can say (x y) 3 = x 3 y 3 3xy (xy) Or, (xy) 3 – 3xy (x y) = x 3 y 3 Or, x 3 y 3 = (x y) {(x




Verify X Y 3 X3 Y3 3xy X Y Brainly In




Algebraic Identities 6 And 7 Youtube
Hint 423 = (40 2)3;Expansion of (x y) 3 is (x y) 3 = x 3 y 3 3 x y (x y) To find out the expansion of (a b c) 3, Put x = a b and y = c So, (a b c) 3 = (x y) 3 (a b c) 3 = x 3 y 3 3 x y (x y) (a b c) 3 = (a b) 3 c 3 3 (a b) c (a b c) Let's calculate (a b) 3 (a b) 3 = a 3 b 3 3 a b (a b) Now, (a b c) 3 = a 3 b 3 3 a b (a b) c 3 3 (a b) c (a b c) (a b c)Called an identity element with respect to if e x = x = x e for all x 2A Example 1 1 is an identity element for multiplication on the integers 2 0 is an identity element for addition on the integers 3 If is de ned on Z by x y = x y 1 Then 1 is the identity 4 The operation de ned on Z by x y = 1 xy has no identity element




Learn Algebraic Identity Of X Y And X Y In 3 Minutes



Factorize X X 3 Y 3 3xy X Y Sarthaks Econnect Largest Online Education Community
Identity Dual Operations with 0 and 1 1 X 0 = X (identity) 3 X 1 = 1 (null element) 2 X1 = X 4 X0 = 0 Idempotency theorem 5 X X = XX x y y is a right identity Then, for all M = a a b b 2S we have that a a b b x x y y = a a b b Multiplying the left hand side we get, ax ay ax ay bx by bx by = a a b b Equating the entries of the matrices leaves the equations ax ay = a and bx by = b ByThe Pauli gates (,,) are the three Pauli matrices (,,) and act on a single qubit The Pauli X,Y and Z equate, respectively, to a rotation around the x, y and z axes of the Bloch sphere by radians The PauliX gate is the quantum equivalent of the NOT gate for classical computers with respect to the standard basis , , which distinguishes the zaxis on the Bloch sphere




Answered Prove The Polynomial Identity For The Bartleby




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
Expand (2x4y)2 using algebraic identity Q 1 Q 2 Divide 6 x3 11 x2 − 39 x − 65 by 3 x2 13 x 13 and find the quotient and remainder Q 3 Q 4 Find the value of 432−43× using a suitable algebraic identity Q 5 Expand (2x4y)2 using algebraic identity403 Authorization Error This server could not verify that you are authorized to access the document requested If you feel you have reached this page in errorRemark 32 Note that an identity (left or right or both) for one operation does not have to be an identity for another operation Think of addition and multiplication let x be an integer Let y be a right inverse of x Then x ∗ y = 1 That is, xy −1 = 1 Solving for y we find y = −x2



Cbse Class 9 Maths Lab Manual Algebraic Identity A B 3 A3 3a2b 3ab2 Cbse Sample Papers




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
Ex 25, 9Verify (i) x3 y3 = (x y) (x2 – xy y2)LHS x3 y3We know (x y)3 = x3 y3 3xy (x y)So, x3 y3 = (x y)3 – 3xy (x y) = (x y)3 – 3xy Karnataka Board Class 9 Maths Chapter 4 Polynomials Ex 45 Question 1 = 9 – 4x 2 Question 2 As per Identity Question 3 Question 4 = 4x 2 y 2 z 2 – 4xy – 2yz 4zx 2 (7b) (c) 2 (c) (3a) = 9a 2 49b 2 c 2 – 42ab – 14bc – 6caX is y, here is results in 1 if id(x) equals id(y) is not Line 2 a and b have same identity Line 3 a and b have same identity Line 4 a= b= 30 Line 5 a and b do not have same identity python_basic_operatorshtm




Ex 2 5 9 Verify I X 3 Y 3 X Y X 2 Xy Y 2 Teachoo




Get The Right Pair Of Algebraic Identities A B A X Y 2 1 X Y X2 Y2 Xy B X2 Y 2 2 Brainly In
Since 3 3 3 3 is too small and 5 3 is too big, one of the numbers (call it y) must be 4 And that leaves x 3 = 91 − 4 3 = 27 , so x=3 In other words, (3,4,5) is the only solution using positive integers, up to permutation If you relax that to allow zero, then (0,0,6) is a solutionPractice with the properties of real numbers The word NUMBERS implies the answer will deal only with numbers The word X implies the answer will contain a variable, but not necessarily the variable x A B Distributive Property (Numbers) 3 (5 2) = 15 6 Commutative Property of Addition (Numbers) 3 7 = 7 3The identity exp(x y) = exp x exp y can fail for Lie algebra elements x and y that do not commute;




Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8




Solved Question 3 We Want To Prove That For All X Y Cu Chegg Com
Simplify (x y) 3 − (x − y) 3 Use the identity x3y3z3−3xyz=(xyz)(x2y2z2−xy−yz−zx) to determine the value of the sum of three integers given the sum of their squares is 110, the sum of their cubes is 684, the product of the three integers is 210, and the sum of any two products (xyyzzx) is 107 Find the value of 533 using the identity (x y)3 = x3 3x2y 3xy2 y3 Hint 533 = (50 3)3;




Solved Questions 1 Demonstrate By Means Of Truth Tables Chegg Com




Learn Algebraic Identities Of X Y And X Y In 3 Minutes
The identity is true for positive integers x, y The LHS and RHS are polynomials in x and y of degree n, so the di erence is a polynomial in x and y of degree at most n, which we want to show is identically 0 Write the di erence as P(x;y) = p 0(x) p 1(x)y p n(x)yn where each pClick here👆to get an answer to your question ️ Using the identity and proof x^3 y^3 z^3 3xyz = (x y z)(x^2 y^2 z^2 xy yz zx)Well x plus y is this entire angle right over here If you look at this right triangle, right triangle ADF, we know that the sine of an angle is the opposite side over the hypotenuse Well the hypotenuse here is one so the sine of this is the opposite over one, or the sine of this angle, the sine of x plus y is equal to the length of this




Solved V Boolean Algebra 1 Derive This Identity X X Y Chegg Com




Ppt Polynomials Powerpoint Presentation Free Download Id
Polynomial Identities When we have a sum (difference) of two or three numbers to power of 2 or 3 and we need to remove the brackets we use polynomial identities (short multiplication formulas) (x y) 2 = x 2 2xy y 2 (x y) 2 = x 2 2xy y 2 Example 1 If x = 10, y = 5a (10 5a) 2 = 10 2 2·10·5a (5a) 2 = 100 100a 25a 2If x x x and y y y are real numbers such that x y = 7 xy=7 x y = 7 and x 3 y 3 = 133 x^3y^3=133 x 3 y 3 = 1 3 3, find the value of x y xy x y Submit your answer 3 3 ( 1640 ) 1 3 \sqrt{\sqrt{\sqrt3{\color{#3D99F6}{}} {\sqrt3{\color{#3D99F6}{} \color{teal}{3(1640) 1}}}}} 3 6 4 0 0 0 3 6 4 0 0 0 3 ( 1 6 4 0 ) 1Learn with flashcards, games, and more — for free



Solved Prove The Identity Sin X Y Sin X Y 2 Cos X Chegg Com




Selina Concise Mathematics Class 8 Icse Solutions Chapter 12 Algebraic Identities Cbse Tuts
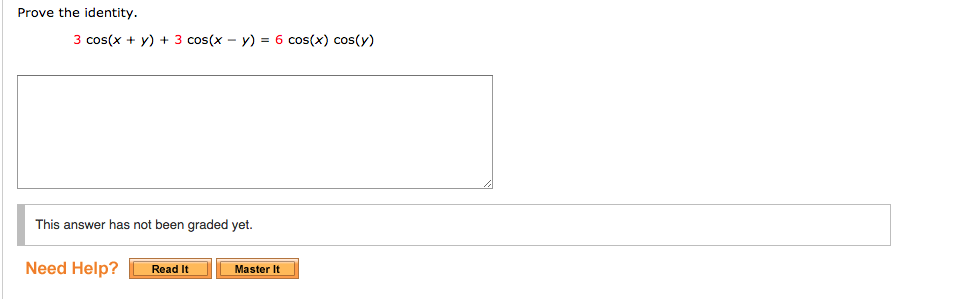
The identity function is a function which returns the same value, which was used as its argument It is also called an identity relation or identity map or identity transformationIf f is a function, then identity relation for argument x is represented as f(x) = x, for all values of x In terms of relations and functions, this function f P → P defined by b = f (a) = a for each a ϵ P, whereProve the identity sin( 1 x) = sin(3 x) Question Prove the identity 3 cos(x y) 3 cos(x y) = 6 cos(x) cos(y) Use a Reciprocal Identity, and then rewrite as a single rational expression 7 tan(x) 7 tan(y) = 7 sin(y) cos(y) cos(x) = cos(x) cos(y) Use an Addition or Subtraction Formula to simplify Prove the identity sin( 1 x #(xy)^3=(xy)(xy)(xy)# Expand the first two brackets #(xy)(xy)=x^2xyxyy^2# #rArr x^2y^22xy# Multiply the result by the last two brackets #(x^2y^22xy)(xy)=x^3x^2yxy^2y^32x^2y2xy^2# #rArr x^3y^33x^2y3xy^2#




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Pdf On The Identity Of Fermat S Equation
Uniqueness works as in Theorem 37, using the inverse for cancellation ifz is another solution to ax = b,thenaz = b = a(a−1b) Multiply on the left by a−1 to get z = a−1az = a−1a(a−1b)=a−1bExample 11 Find the expansion of the following using suitable identity (i) (3x 7y) (3x – 7y) (ii) 4 43 54 5 4 xy x y Solution (i) (3x 7y) (3x – 7y) Since (a b) (a – b) = a2 – b2, therefore(3x 7y) (3x – 7y) = (3x)2 – (7y)2 = 9x2 – 49y2 (ii) 4 43 54 5 4 Since x − y = 3 xy=3 x − y = 3 implies y = x − 3, y=x3, y = x − 3, substituting this into the given identity gives a x (x − 3) b x c (x − 3) 9 = 0 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 \begin{aligned} ax(x3)bxc(x3)9&=0\\ ax^2(3abc)x3(c3)&=0 \end{aligned} a x (x − 3) b x c (x − 3) 9 a x 2 (− 3 a b c) x − 3 (c − 3) = 0 = 0




Algebraic Expressions And Identities Class 8 Maths Geeksforgeeks




Learn Algebraic Identity Of X Y And X Y In 3 Minutes
Solution (x 3 8y 3 27z 3 – 18xyz)is of the form Identity VIII where a = x, b = 2y and c = 3z So we have, So we have, (x 3 8y 3 27z 3 – 18xyz) = (x) 3 (2y) 3 (3z) 3 – 3(x)(2y)(3z)= (x 2y 3z)(x 2 4y 2 9z 2 – 2xy – 6yz – 3zx)This algebraic identity can be written in the following form too ( a − b) 3 = a 3 − b 3 − 3 a 2 b 3 a b 2 Generally, the a minus b whole cubed algebraic identity is called by the following three ways in mathematics The cube of difference between two terms identity or simply the cube of difference identity The cube of a binomial formulaThe Baker–Campbell–Hausdorff formula supplies the necessary correction terms Transcendency The function e z is not in C(z) (that is, is not the quotient of




Experiment No 2 Boolean Algebra




Algebraic Identities Of Polynomials A Plus Topper




Companion Website Example Of Information Displayed If The Identity Download Scientific Diagram



Koreascience Or Kr




Example 11 Using Identity I Find 2x 3y 2 Algebra Class 8




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Solved 3 Simplify The Following Functional Expressions Chegg Com



Find The Following Squares By Using Identities I B 7 2 Ii Xy 3z 2 Sarthaks Econnect Largest Online Education Community




Using Identities Prove That X Y Z 2 Is Greater Than Or Equal To 3 Xy Yz Zx Maths 419 Meritnation Com




Solved Prove The Identity 3 Cos X Y 3 Cos X Y 6 Chegg Com




X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X 2 X3 Y3 Z3 3xyz Mathematics Topperlearning Com T86qex55



Identity Vs Equation Acute Angel




Rational Functions And Endomorphisms Separable Endomorphisms Parallelogram Identity And Degree Map




Which Of The Following Is A Factor Of X Y 3 X 3 Y 3




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf




X Y 3 2 X Y 3 2 Solve By Using Suitable Identity Brainly In




If X Y 26 And Xy 3 Find The Value Of X Y 4y 2 A A 4yi If 26 And 3 Maths Algebraic Expressions And Identities Meritnation Com
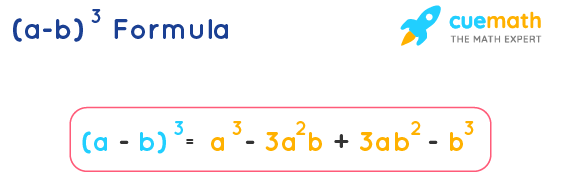



A Minus B Whole Cube Formula Examples A B 3 Formula




Using Identity Viii X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Solve The Following Question 8x3 Y3 27z3 18xyz Maths Polynomials Meritnation Com




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Algebraic Identities Of Polynomials A Plus Topper
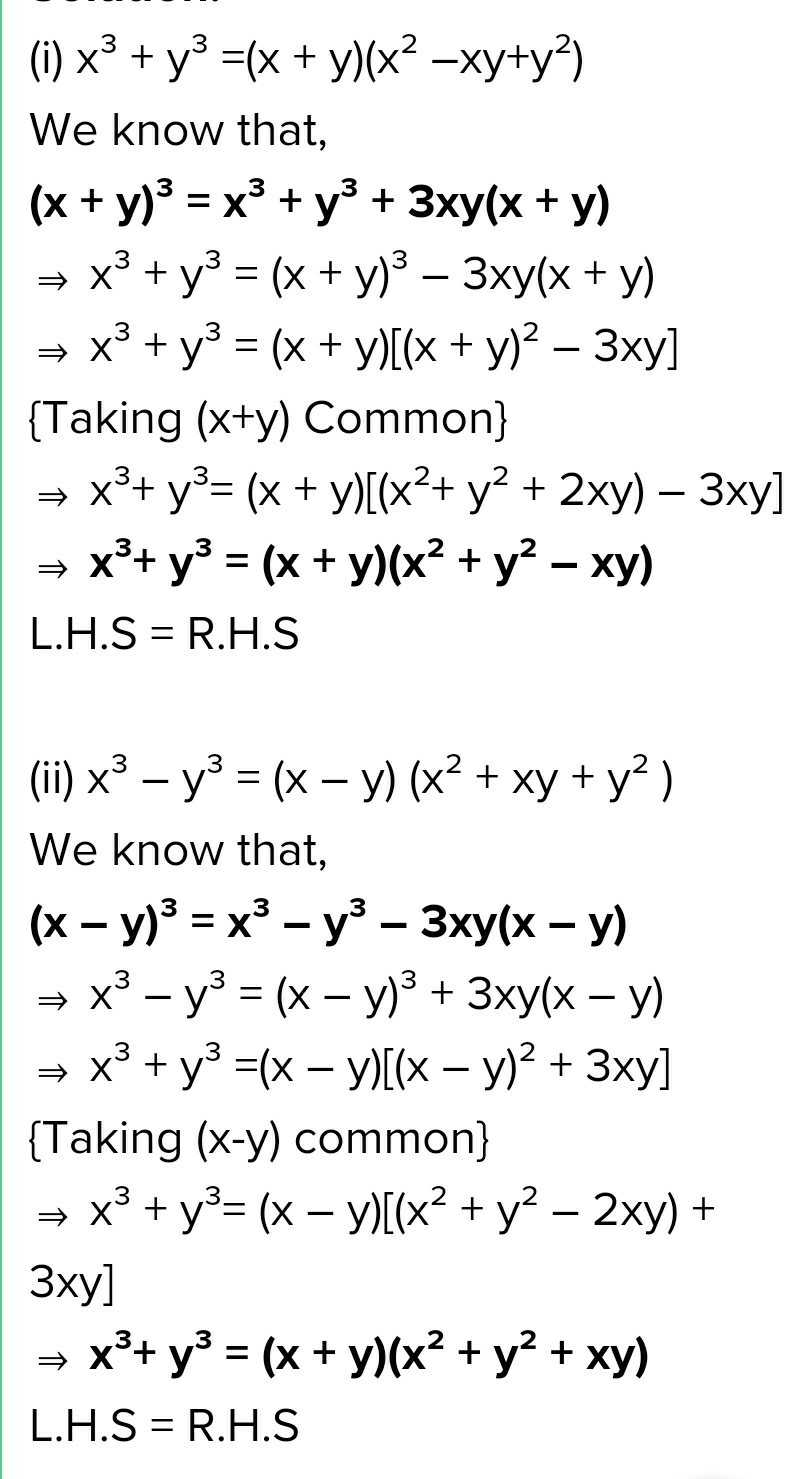



9 Verify I X3 Y3 X Y X2 Xy Y Ii P X Y X2 Xy Scholr




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




2 Solve It Plz Q If X Y 10 And Xy 21 Find The Value Of X3 Y3 Using Identity Maths Polynomials Meritnation Com




Cos X Y Formula Proof Iventania




How To Verify Algebric Identity X Y 3 X3 3xy X Y Y3 Maths Polynomials Meritnation Com




Pdf Antiflexible Rings With Identity X Y X 0 M Hema Prasad Academia Edu



2




Ex 2 5 12 Verify That X3 Y3 Z3 3xyz 1 2 Ex 2 5




Derive An Identity For X Y 3 Brainly In
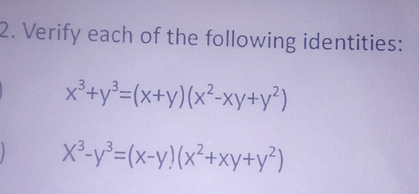



2 Verify Each Of The Following Identities X3 Y3 X Y X2 X Scholr




Expert Answer What Are The Factors Of X Y 3 X3 Y3 Brainly In



Expand 1 X Y 3 Whole Cube Studyrankersonline




If X 3 A N D Y 1 Find The Values Of Each Of The Using Identity X 7 Y 3 X 2 49 Y 2 9 X Y 21




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




Solved Cos X Y 3 Verify The Identity 1 Tan X Tany Chegg Com




Darlene Wrote This Proof Of The Identity X Y 2 X Y 2 4xy Which Of The Following Is A Justification For Step 5 Of




Find The Following Squares By Using The Identities I B 7




153 Pm Lte 404 1 D D Df See How To Solve It At Qanda




List Of Trigonometric Identities Wikipedia




It Some Algebraic Identities Are Given Below Ti I X Y Scholr




Factorise 27 X Y 3 8 X Y 3 Maths Polynomials Meritnation Com
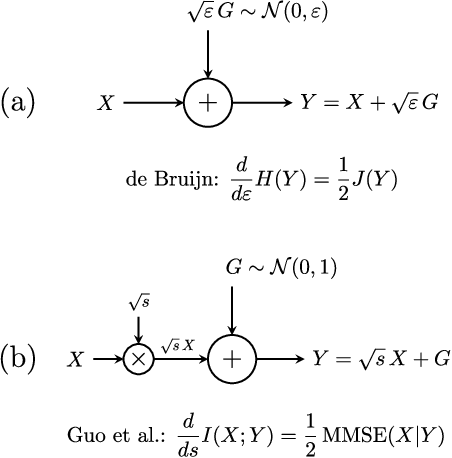



Pdf Generalization Of The De Bruijn Identity To General Phi Entropies And Phi Fisher Informations Semantic Scholar



1
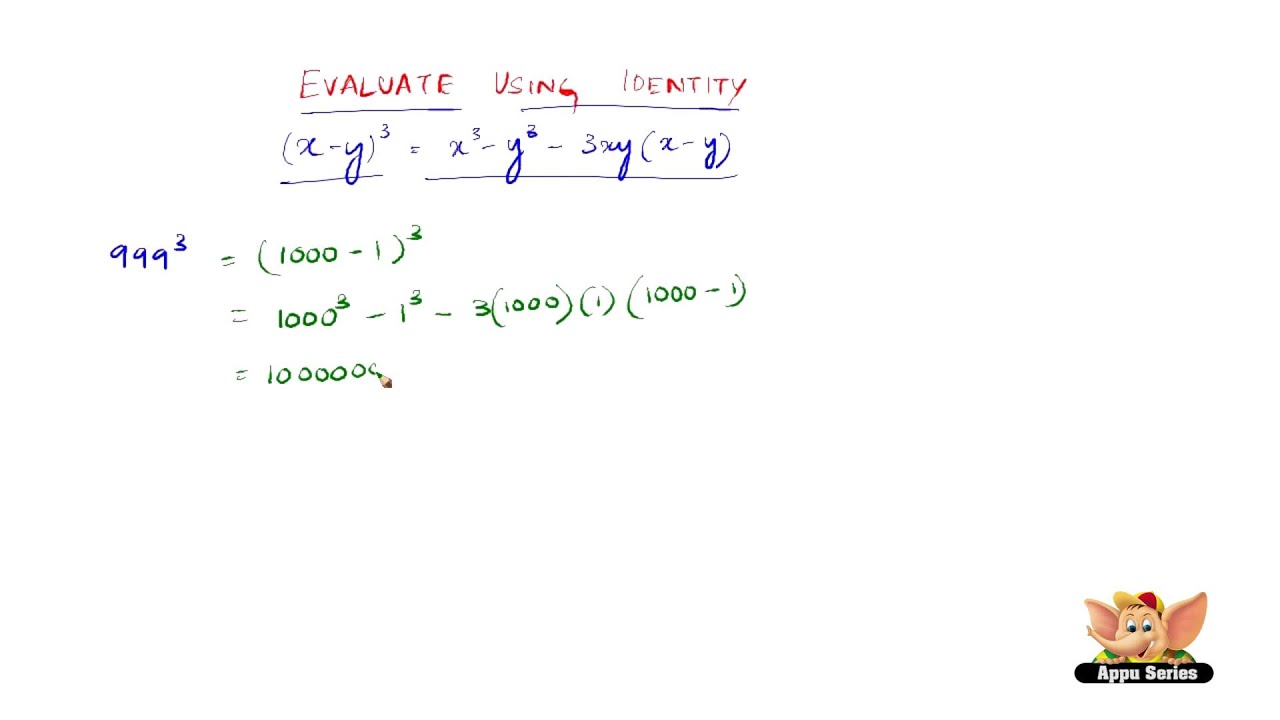



How To Evaluate Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Symmetric Polynomial Identities X Y Z N In Terms Of Sigma 1 X Y Z Sigma 2 Xy Yz Xz And Sigma 3 Xyz Mathematics Stack Exchange



Identity Mathematics Wikipedia




Pdf Two Theta Function Identities Of Level 10




Ex 9 5 3 Find B 7 2 Using Algebra Identities Teachoo




Predicate Logic Translation Gregory Chapter 5 3 5




Pdf On Trace Forms On A Class Of Commutative Algebras Satisfying An Identity Of Degree Four




Chapter 7 Spectral Theory Of Linear Operators In Normed Spaces



2




Untitled Bingo Card




Math Garden Binomial Identity




Ppt Polynomials Powerpoint Presentation Free Download Id




Ex 9 4 3 V Simplify X Y 2x Y X 2y X Y Class 8



1




Solved Prove The Identity 3 Cos X Y 3 Cos X Y 6 Cos X Chegg Com
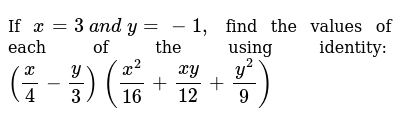



If X 3 A N D Y 1 Find The Values Of Each Of The Using Identity X 4 Y 3 X 2 16 X Y 12 Y 2 9
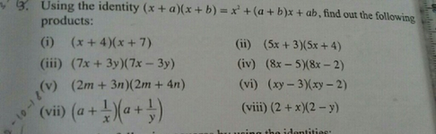



V3 Using The Identity X A X B X A B X Ab Find Ou Scholr




Prove X Y 3 Y Z 3 Z X 3 3 X Y Y Z Z X Brainly In



1




If X 3 A N D Y 1 Find The Values Of Each Of The Using Identity X 7 Y 3 X 2 49 Y 2 9 X Y 21




Let G X E R X 1 Be The Set Of All Real Numbers Greater Than 1 For X Y E G Define X Y Xy X Y 2 1 Show That The Operation Is




Ex 9 3 3 Find The Product I A 2 2a 22 4a 26 Algebra




Solved 6 2 2 4 Points 1 2 5 6 A If X And Y Find Xy Chegg Com



1



If X Y 12 And Xy 27 Then Find The Value Of X3 Y3 Polynomials Maths Class 9




Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 5 Polynomials




Algebraic Identities Of Polynomials A Plus Topper




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Given A X 3 Y 3 If A 3i Where I Is The Identity Matrix Of Order 2 Find X And Y Brainly In




Learn Algebraic Identity Of X Y And X Y In 3 Minutes




How To Expand Using The Identity X Y 3 X3 Y3 3x2y 3xy2 Youtube




Polynomials Ppt Video Online Download




X 3 Y 3 X 3 Y 3 Formula Proof Youtube



0 件のコメント:
コメントを投稿